Poisson Distribution Introduction YouTube

Distribución de Poisson Ejemplo 2 YouTube

La fórmula de distribución de Poisson está dada por: {eq}P(X=k)=\frac{\lambda^{k}e^{-\lambda}}{k!} {/eq} donde {eq}\lambda {/eq} es la tasa promedio constante de ocurrencia del evento, y {eq}k {/eq} es la cantidad de eventos exitosos. La distribución de Poisson se puede aplicar a una amplia variedad de dominios, incluidas las ciencias.

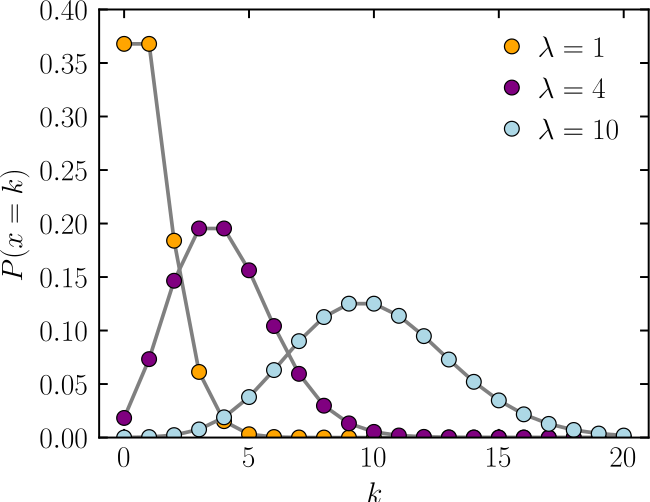
Distribución de Poisson Wikipedia, la enciclopedia libre

Fórmula y ecuaciones. La forma matemática de la distribución de Poisson es la siguiente: - La variable aleatoria es y. - μ (también a veces denotado como λ) es la media o parámetro de la distribución. - Número de Euler: e = 2.71828. - La probabilidad de obtener y = k es P. - k es el número de éxitos 0, 1,2,3….

Distribución de Poisson Ejemplos resueltos YouTube

Distribución binomial — La distribución binomial es una distribución discreta de dos parámetros que cuenta el número de éxitos en N pruebas independientes con la probabilidad de éxito p.La distribución de Poisson es el caso limitante de una distribución binomial donde N se acerca a infinito y p a cero mientras Np = λ.Consulte Comparar las pdf de la distribución binomial y de Poisson.

DISTRIBUCIÓN POISSON EJEMPLO YouTube

Tenga en cuenta que la distribución de Nt depende de los parámetros r y t sólo a través del producto rt. La distribución se denomina distribución de Poisson con parámetro rt. En el experimento de Poisson, variar r y t con las barras de desplazamiento y anotar la forma de la función de densidad de probabilidad.

Ejemplo Distribución de Poisson YouTube

A Poisson distribution is a discrete probability distribution. It gives the probability of an event happening a certain number of times ( k) within a given interval of time or space. The Poisson distribution has only one parameter, λ (lambda), which is the mean number of events. The graph below shows examples of Poisson distributions with.

Poisson Distribution

Fórmula y ecuaciones. La forma matemática de la distribución de Poisson es la siguiente: - μ (también a veces denotado como λ) es la media o parámetro de la distribución. - Número de Euler: e = 2.71828. - La probabilidad de obtener y = k es P. - k es el número de éxitos 0, 1,2,3…. - n es el número de pruebas o eventos.

PROBABILIDAD Y ESTADÍSTICA DISTRIBUCIÓN DE PROBABILIDAD POISSON

Hay dos características principales de un experimento de Poisson. La distribución de probabilidad de Poisson da la probabilidad de que se produzca un número de eventos en un intervalo fijo de tiempo o espacio si estos eventos se producen con una tasa promedio conocida y con independencia del tiempo transcurrido desde el último evento. Por ejemplo, un editor de libros podría estar.

📚 Distribución de poisson ejercicios resueltos

Usando la distribución de Poisson: Calcular μ = np = 200(0.0102) ≈ 2.04. P(x = 10) = poissonpdf(2.04, 10) ≈ 0.000045. Esperamos que la aproximación sea buena porque n es grande (mayor que 20) y p es pequeña (menos de 0.05). Los resultados son cercanos, ambas probabilidades reportadas son casi 0. Ejercicio 4.7.7.

DISTRIBUCIÓN POISSON EXPLICACIÓN Y EJERCICIO PASO A PASO YouTube

The Poisson distribution is often used in quality control, reliability/survival studies, and insurance. Data are counts of events (nonnegative integers with no upper bound). All events are independent. Average rate does not change over the period of interest. The following graphs represent Poisson distributions with different lambdas.

PROBABILIDAD Y ESTADÍSTICA DISTRIBUCIÓN DE PROBABILIDAD POISSON

Actualizado el 1 octubre 2020. La distribución de Poisson es una distribución de probabilidad discreta que modeliza la frecuencia de eventos determinados durante un intervalo de tiempo fijado a partir de la frecuencia media de aparición de dichos eventos. En otras palabras, la distribución de Poisson es una distribución de probabilidad.

Poisson Distribution Formula Calculator (Examples with Excel Template)

Las distribuciones de Poisson se utilizan para encontrar la probabilidad de que ocurra un evento en un intervalo de tiempo, área, volumen o distancia. Las distribuciones de Poisson se pueden aplicar a muchos campos de estudio, incluidos la ciencia y los negocios. Por ejemplo, un gerente comercial puede usar una distribución de Poisson para.

Poisson Distribution Formula and Meaning in Finance

La distribución de Poisson fue propuesta por primera vez por Simeón Poisson en libro publicado en 1837. A medida que pasaron los años, el número de aplicaciones comenzó a aumentar, sobre todo el siglo XX y con la aparición de las computadoras en el siglo XXI permitió incrementarlas aún más. La distribución de Poisson es una.

Distribucion Poisson YouTube

Calcular probabilidades de la distribución de Poisson paso a paso. La calculadora encontrará las probabilidades simples y acumulativas, así como la media, la varianza y la desviación estándar de la distribución de Poisson. Tasa media de éxito \lambda λ: Valor de una variable aleatoria X X: Si la calculadora no calculó algo o ha.

PPT Distribución de Probabilidad Poisson PowerPoint Presentation, free download ID4240046

Hoy revisamos la distribución de Poisson, con un repaso de teoría y ejercicios resueltos. ️ Todos los videos de Poisson: https://www.youtube.com/playlist?li.

Video de la distribución de Poisson, su esperanza y varianza YouTube

Ejemplos y fórmula del proceso de Poisson. Ejemplo 1. Estos son ejemplos de eventos que pueden describirse como procesos de Poisson: Mi computadora falla en promedio una vez cada 4 meses. Las urgencias hospitalarias reciben una media de 5 casos muy graves cada 24 horas. El número de coches que pasan por un punto, en una carretera pequeña, es.

PROBABILIDAD Y ESTADÍSTICA DISTRIBUCIÓN DE PROBABILIDAD POISSON

El eje horizontal es el índice k. En teoría de probabilidad y estadística, la distribución de Poisson es una distribución de probabilidad discreta que expresa, a partir de una frecuencia de ocurrencia media, la probabilidad de que ocurra un determinado número de eventos durante cierto período de tiempo. Concretamente, se especializa en.