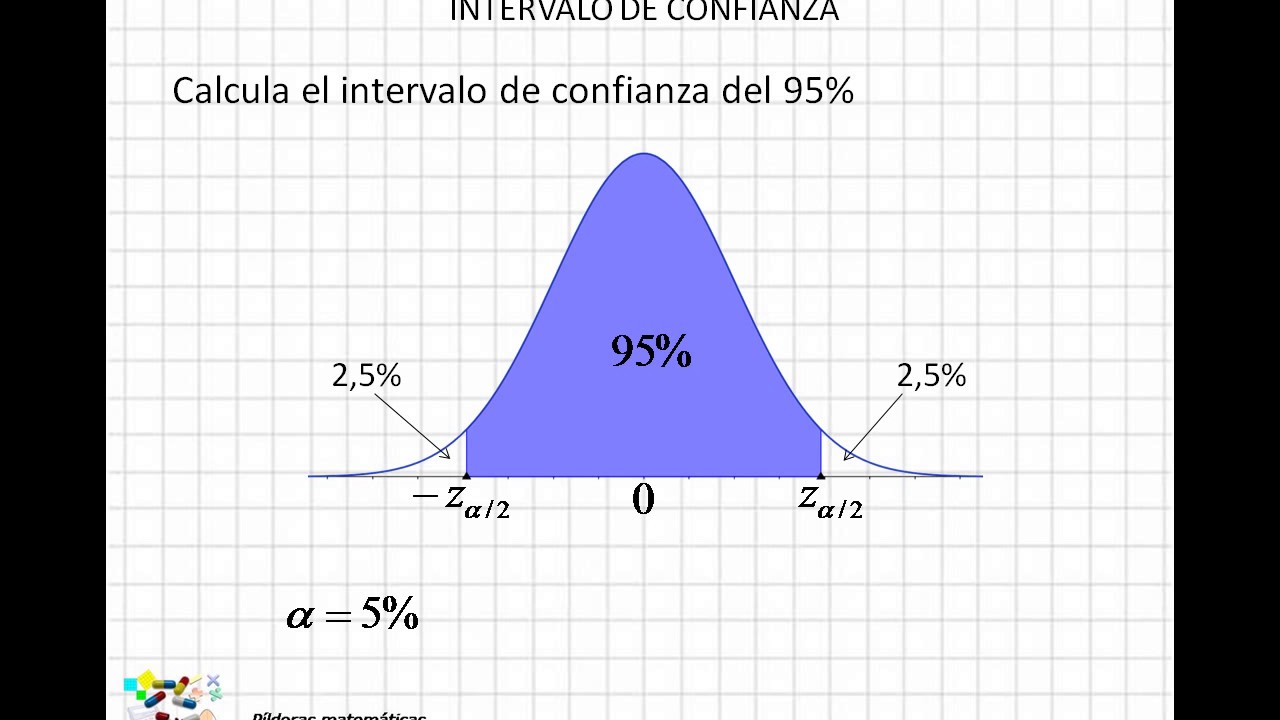
Intervalo de Confianza para una Media (muestras pequeñas y/o se desconoce la varianza

07 Intervalo de confianza YouTube

Indica el nivel de confianza. Por defecto, confianza = 0.95 (95 por ciento) grafico. Es un valor lógico. Por defecto grafico = FALSE. Si se quiere obtener una representación gráfica del intervalo de confianza obtenido, cambiar el argumento a grafico = TRUE. Nota: Esta opción no está implementada para todos los casos.

Distribución de la media muestral (t de Student) Ejercicio YouTube

Cuando α = 0.05, confiamos que μ pertenezca a dicho intervalo, con un nivel de confianza del 95%. 13.3 TAMAÑO DE MUESTRA NECESARIO PARA LA OBTENCIÓN DE UN INTERVALO DE CONFIANZA PARA LA MEDIA DE UNA POBLACIÓN NORMAL CON LONGITUD PREFIJADA. La longitud del intervalo de confianza dado por la ecuación (2) es. n z.

ejemplo 1 2 intervalos de confianza para la media YouTube

8.S: Intervalos de Confianza (Resumen) En este módulo aprendimos a calcular el intervalo de confianza para una sola media poblacional donde se conoce la desviación estándar poblacional. En este capítulo, aprenderás a construir e interpretar intervalos de confianza. También aprenderás una nueva distribución, el Student's-T, y cómo se.

Educatina Intervalo de confianza para la media con variancia conocida

4.2 Intervalo de confianza para la media.. Suponemos que los datos proceden de una distribución normal. Para calcular un intervalo de confianza de nivel 0.95 para la duración media del proceso usamos el comando t.test: t.test (resultados) $ conf.int # 95% es el nivel por defecto #> [1].

INTERVALOS DE CONFIANZA PARA LA MEDIA POBLACIÓN FINITA ESTADÍSTICA MATEMÁTICA PROBLEMA 1

Por lo tanto, la fórmula para calcular el intervalo de confianza para la media es la siguiente: Para tamaños muestrales grandes y un nivel de confianza del 95% el valor crítico es Z α/2 =1,96 y para un nivel de confianza del 99% el valor crítico es Z α/2 =2,576. La fórmula anterior se utiliza cuando la varianza de la población es conocida.

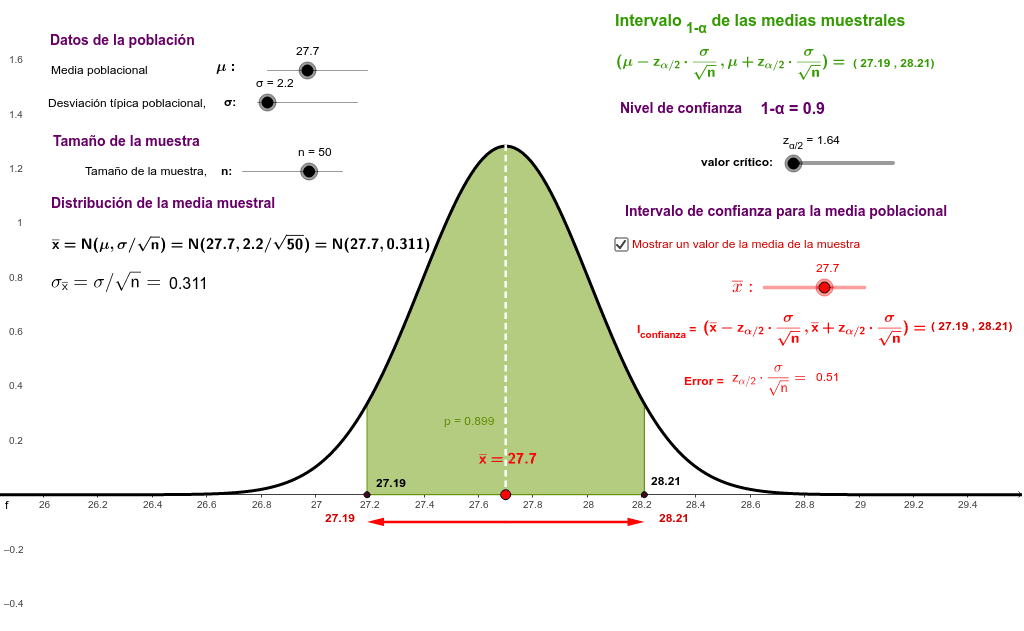
Intervalo de confianza para la media GeoGebra

Con este vídeo aprenderás qué son lo intervalos de confianza para la media y cómo se calculan.En este caso veremos intervalos de confianza para la media cuan.

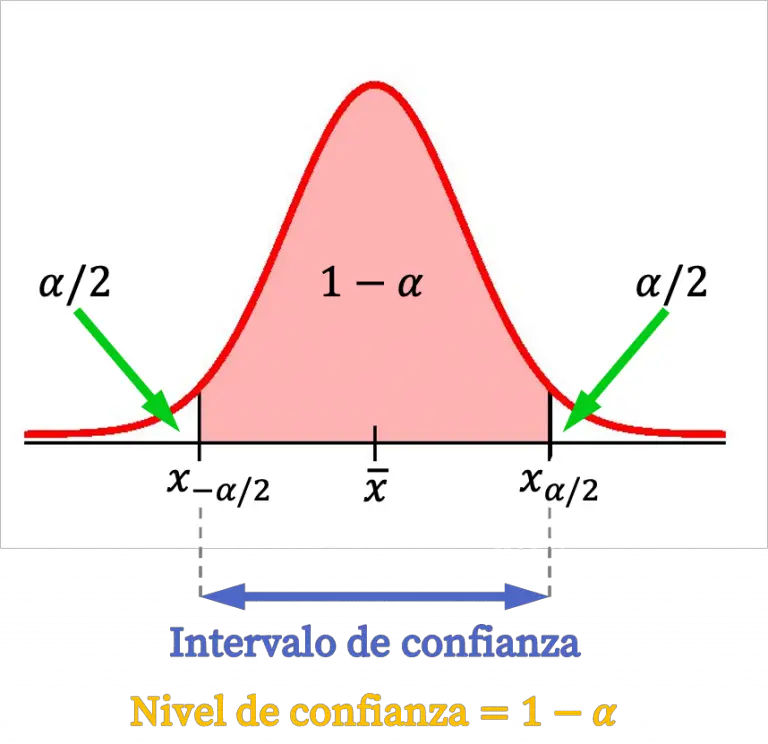
Intervalo de confianza para la media Probabilidad y Estadística

La forma general para un intervalo de confianza para una sola población media, desviación estándar conocida, distribución normal viene dada por. (lower bound, upper bound) = (point estimate- EBM, point estimate + EBM) = ˉx − EBM, ˉx + EBM. = (ˉx − z σ √n, ˉx + z σ √n)

Ejemplo de cálculo de intervalo de confianza para la estimación de una media poblacional

Un intervalo de confianza para la media nos da un rango de valores admisibles para la media de la población. Si un intervalo de confianza no incluye un valor determinado, podemos decir que no es probable que el valor particular sea la media verdadera de la población. Sin embargo, incluso si un valor está dentro del intervalo, no debemos.

6 4 4 Intervalo de confianza para la proporción YouTube

Tema 3 - Intervalos de confianza. Definiciones básicas. Una estimación por intervalos de un parámetro poblacional es una regla para calcular, a partir de una muestra, un intervalo en el que, con una cierta probabilidad (nivel de confianza), se encuentra el valor verdadero del parámetro. Estas reglas definirán, a su vez, estimadores.

Intervalo de Confianza para una Media (muestras pequeñas y/o se desconoce la varianza

Definición. Un intervalo de () % de confianza para la estimación de un parámetro poblacional que sigue una determinada distribución de probabilidad, es una expresión del tipo [,] tal que ⁡ [] = donde es la función de distribución de probabilidad de .. Ejemplos Intervalo de confianza de la media de una población. De una población con media y desviación típica se pueden tomar.

Estimación por intervalos qué es, ejemplos y ejercicios resueltos

Las condiciones que necesitamos para la inferencia en una media son: Aleatoriedad: debe utilizarse una muestra aleatoria o un experimento aleatorizado para obtener los datos. (la media de la muestra) debe ser aproximadamente normal. Esto se cumple si nuestra población padre es normal o si la muestra es razonablemente grande ( n ≥ 30)

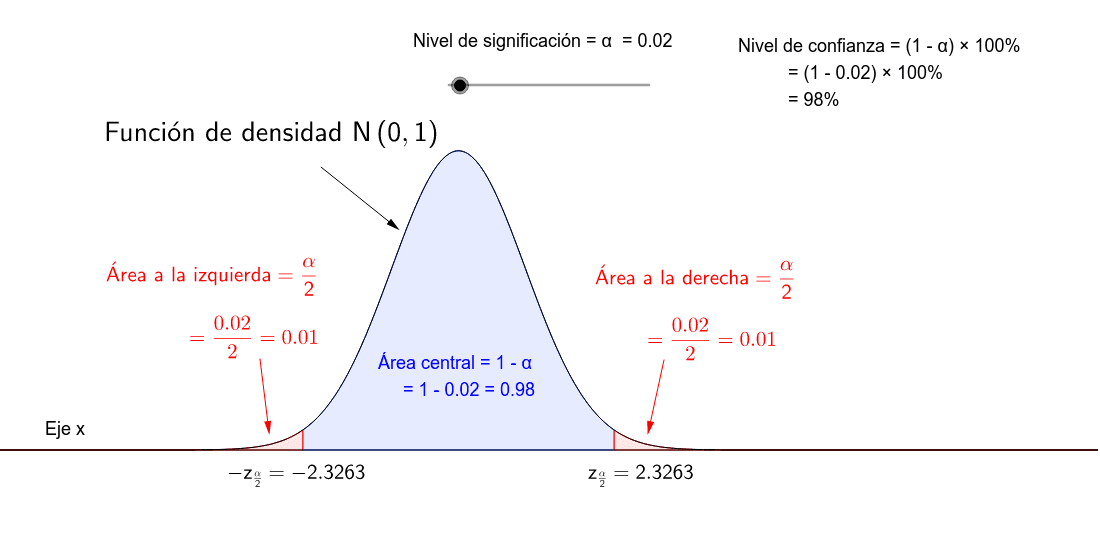
IC media de la Normal (sigma conocida) cuantiles GeoGebra

Un intervalo de confianza para una media poblacional con una desviación estándar poblacional conocida se basa en la conclusió n del Teorema del L. Esto se puede encontrar usando una computadora, o usando una tabla de probabilidad para la distribución normal estándar. Debido a que los niveles comunes de confianza en las ciencias sociales.

INTERVALO DE CONFIANZA PARA LA MEDIA YouTube

Por lo tanto, para poder calcular el intervalo de confianza para la media poblacional vamos a tipificar los valores de x1 y x2 para transformarlos en -z de α/2 y z de α/2 y poder así utilizar la tabla de distribución normal N (0,1): Tipificamos el valor de x1, teniendo en cuenta que la media es la media muestral y la desviación típica se.

Inferencia Intervalo de confianza YouTube

Más sobre los intervalos de confianza Hay un par de cosas a tener en cuenta para interpretar mejor los resultados obtenidos con esta calculadora: Un intervalo de confianza es un intervalo (correspondiente al tipo de estimadores de intervalo) que tiene la propiedad de que es muy probable que el parámetro de población esté contenido por este intervalo (y esta probabilidad se mide por el.

PPT Estimación e intervalos de confianza PowerPoint Presentation, free download ID1118526

Usamos la siguiente fórmula para calcular un intervalo de confianza para una media: Intervalo de confianza = x +/- z * (s / √ n ) dónde: El valor z que utilizará depende del nivel de confianza que elija. La siguiente tabla muestra el valor z que corresponde a las opciones de nivel de confianza más populares:

Intervalo de Confianza Distribución Muestral de Medias YouTube

El siguiente paso es encontrar el valor de t. Como puede ver en Tabla 10.7.1, el valor para el 95% intervalo para df = N − 1 = 4 es 2.776. El intervalo de confianza se calcula entonces tal como es cuando σM. Las únicas diferencias son eso sM y t más bien que σM y Z se utilizan. Lower limit = 5 − (2.776)(1.225) = 1.60.