Máximos y Mínimos por el Método de la segunda derivada Mapa Mental

Encontrar máximos y mínimos de una función mediante la segunda derivada YouTube

Aprende gratuitamente sobre matemáticas, arte, programación, economía, física, química, biología, medicina, finanzas, historia y más. Khan Academy es una organización sin fines de lucro, con la misión de proveer una educación gratuita de clase mundial, para cualquier persona en cualquier lugar.

CRITERIO DE LA SEGUNDA DERIVADA PARA ENCONTRAR LOS MÁXIMOS Y MÍNIMOS DE UNA FUNCIÓN YouTube

Objetivos de aprendizaje. 4.7.1 Utilizar las derivadas parciales para localizar los puntos críticos de una función de dos variables.; 4.7.2 Aplicar una prueba de segunda derivada para identificar un punto crítico como máximo local, mínimo local o punto de silla para una función de dos variables.; 4.7.3 Examinar los puntos críticos y los puntos límite para calcular los valores máximos.

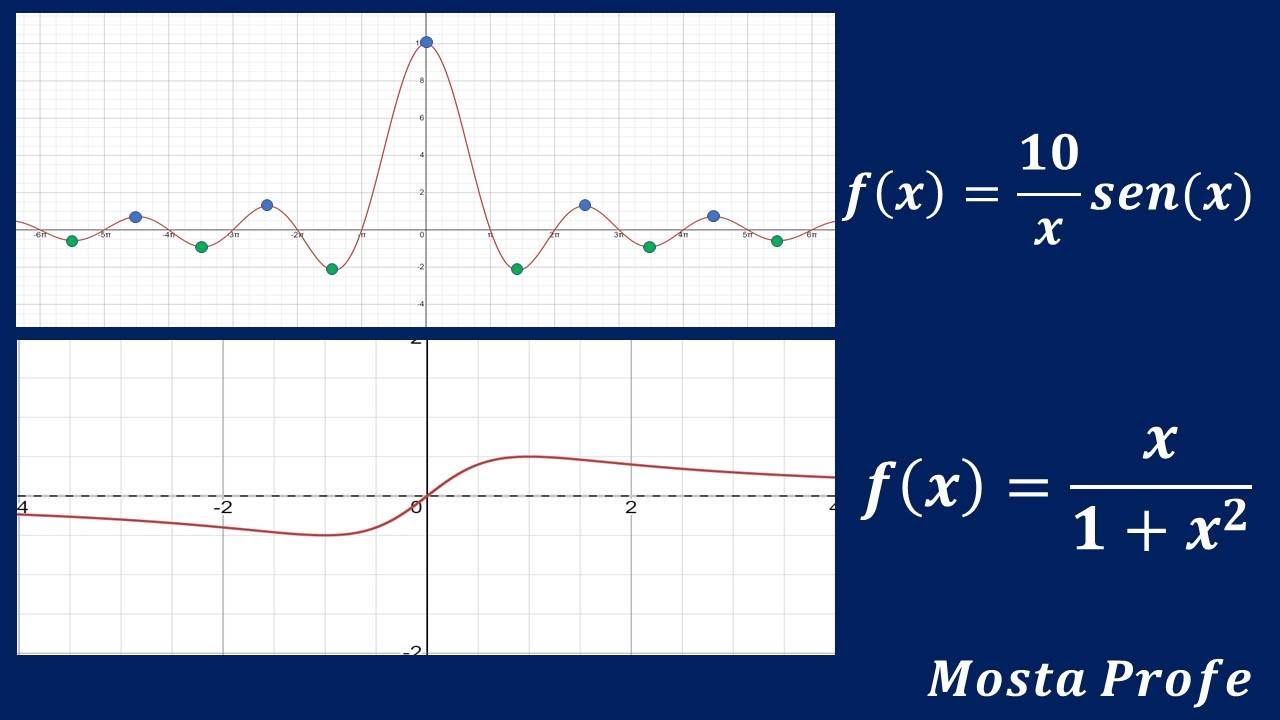
Cómo hallar Extremos Máximos y Mínimos de Función Racional Primera y Segunda Derivada YouTube

La aplicación directa del criterio de la segunda derivada es determinar si los puntos críticos de una función (puntos que anulan la primera derivada) son máximos o mínimos. Si hay extremos, podemos deducir la monotonía de la función alrededor de éstos. Además de esto, los puntos que anulan la segunda derivada son candidatos a ser.

TEORIA APLICACIÓN DE LA DERIVADA MAXIMOS Y MINIMOS YouTube

También se tiene que -2 y 2 son números críticos de la segunda derivada de la función f(x). Del mismo modo, f′′ (x) = x2 − 4 es decreciente en el intervalo (−∞, 0) y creciente en el intervalo (0, ∞), por lo que la primera derivada f′ (x) tiene un punto de inflexión en (0, 0). Los números críticos de la primera derivada f.

Máximos y Mínimos por el Criterio de la Segunda Derivada YouTube

Apóyanos con una donación y obtén recompensas exclusivas https://vitual.lat/donacion/ En este video se explica paso a paso máximos y mínimos de una función.

Máximos y mínimos (Criterio de la segunda derivada) YouTube

En este vídeo veremos como encontrar máximos o mínimos de una función aplicando el criterio de la segunda derivada. Particularmente en este ejemplo, en el cu.

Cálculo de Máximos y Mínimos de Función Polinomial utilizando Primera y Segunda Derivada [1

En este video encontraremos el máximo y el mínimo de una función mediante el criterio de la segunda derivada. Primero encontraremos los puntos críticos con l.

Máximos y mínimos absolutos Aplicaciones de la derivada La Prof Lina M3 YouTube

Te doy la bienvenida a la clase digital 15 del curso Cálculo Diferencial en la que estudiaremos el tema Criterio de la segunda derivada (Máximos y mínimos). En esta clase vamos a abordar el tema del criterio de la segunda derivada. Es importante recordar que es un teorema o método del cálculo diferencial, en el cual se usa la segunda.

CD.29 Criterio de la segunda derivada para máximos y mínimos. Concavidad y gráfico. Ejemplo 2

Máximos y mínimos: criterio de la segunda derivada. Aprenderás a clasificar los puntos críticos de una función como máximos, mínimos o puntos de inflexión con base en la segunda derivada. Ahora que sabemos que la segunda derivada nos da información acerca de la primera derivada, vamos a utilizarla para calcular los máximos y mínimos.

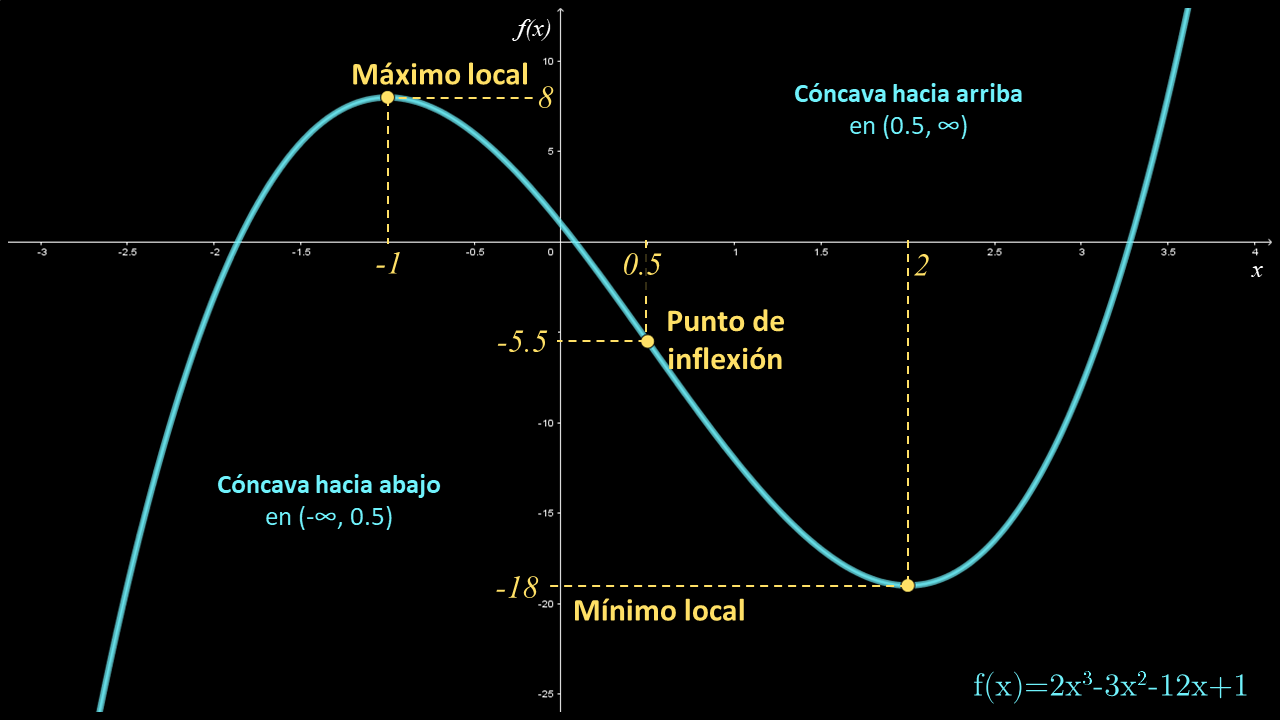
Criterios de la segunda derivada

SUSCRÍBETE: http://bit.ly/VN7586 (NO OLVIDES DAR UN ¨LIKE¨)VISITA: http://math2me.comFB: http://bit.ly/FBmath2meG+: http://google.com/+math2meTwitter: http:/.

Criterio de la segunda derivada Ejemplos YouTube

Paso 3: Encuentra la segunda derivada. Después de encontrar los puntos críticos, es hora de determinar si son máximos o mínimos utilizando la segunda derivada. Calcula la segunda derivada de la función original y evalúa los puntos críticos encontrados en el paso anterior. Si la segunda derivada evaluada en un punto crítico es positiva.

Clase digital 15 Criterio de la segunda derivada (Máximos y mínimos) Recursos Educativos Abiertos

Máximos y mínimos usando el criterio de la segunda derivada, concavidad y puntos de inflexión. Mas videos de calculo diferencial en el canal de profesor part.

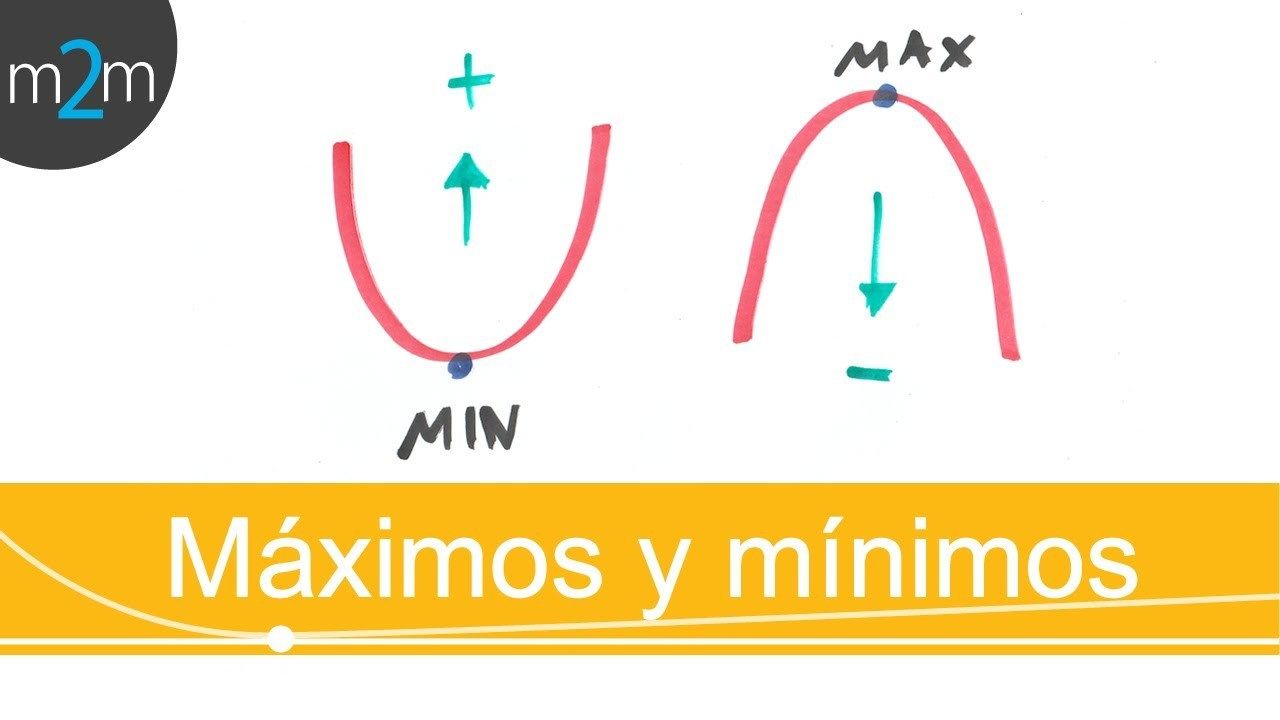
Máximos y Mínimos por el Método de la segunda derivada Mapa Mental

Regla de la segunda derivada. Problemas resueltos. 1. Definición de extremo. Intuitivamente, un punto a a es un máximo relativo de la función f f si f (a) ≥ f (x) f ( a) ≥ f ( x) para los x x cercanos a a a. Es un mínimo relativo si f (a) ≤ f (x) f ( a) ≤ f ( x).

Criterio de la Segunda Derivada para Máximos y Mínimos locales YouTube

El Criterio de la segunda derivada es un teorema o método de cálculo matemático en el que se utiliza la segunda derivada para efectuar una prueba correspondiente a los máximos y mínimos relativos de una función.. Se basa en el hecho de que si la gráfica de una función es convexa en un intervalo abierto que contiene a , y ′ =, debe ser un mínimo relativo a .

Cómo encontrar los puntos MÁXIMOS y MÍNIMOS de una función DERIVADA primera y DERIVADA segunda

Los máximos y mínimos de una función pueden encontrarse mediante la derivada. Si la función está definida en un intervalo (a, b) y es derivable en él, para que haya un punto extremo local ( máximo o mínimo) c del intervalo), la derivada primera en c debe ser nula, f' (c) = 0. Esta condición es necesaria, pero no suficiente.

Ejercicio de máximos y mínimos por SEGUNDA DERIVADA YouTube

En este vídeo veremos como encontrar máximos y mínimos aplicando el criterio de la segunda derivada, veremos como un punto crítico se convierte en un punto d.