Reglas de inferencia logica ejercicios resueltos modus ponendo y tollendo ponens YouTube

TOLLENDO PONENS EXPLICACIÓN YouTube

Do you want to learn how to reason logically and critically? This webpage introduces you to some common patterns of valid arguments, such as modus ponens, modus tollens, and hypothetical syllogism. You will also find examples and exercises to test your understanding of these concepts. This webpage is part of a miniguide to critical thinking, a free online resource by Humanities LibreTexts.

Reglas de inferencia lógica Ejercicios Modus Ponens, Modus Tollens, Silogismo, Modo Disyuntivo

The precedent studies on the validity of Modus ponens and Modus tollens have been carried out with most regard to a major type of conditionals in which the conditional clause is a sufficient condition for the main clause. But we sometimes, in natural language arguments, find other types of conditionals in which the conditional clause is a necessary or necessary and sufficient condition for the.

Modus Ponens The following valid arguments show us

Modus Tollens: If X, then Y. Not Y. Therefore, not X. You saw the first form, disjunctive syllogism, in the previous example. The second form, modus ponens, uses a conditional, and if you think about necessary and sufficient conditions already discussed, then the validity of this inference becomes apparent. The conditional in premise 1.

REGLAS DE INFERENCIA LOGICA MODUS TOLLENDO PONENS YouTube

MODUS PONENS AND MODUS TOLLENS 107 Conﬁrmation.Given P(h/e)=x and p(e)=y >0, letting P(h)=z leads to the probability distribution, e ∼e h xy z-xy ∼h y(1−x) 1−[z+y(1−x)] A probability distribution is an assignment of probabilities, i.e. numbers not less than 0 nor greater than 1, to all members of a logical partion of propositions, which probabilities sum

Modus Ponens y Modus Tollens (Reglas de Inferencia) YouTube

Inference. Let's call a proposition with known truth value to be a fact. Establishing the truth value of some proposition from the given facts is called inference. Start Free Trial. Learn about inference, correct argument types, and deductive reasoning.

MODUS TOLLENDO TOLLENS (REGLAS DE INFERENCIA) CON EJEMPLOS YouTube

Modus ponens is a rule of inference in formal logic expressed through a conditional syllogism that takes the following form: To understand modus ponens, it's crucial to understand the difference between these key elements: Antecedent: The first part of a conditional statement, following "if.". It is the condition that triggers the outcome.

MODUS TOLLENDO PONENS (REGLAS DE INFERENCIA) CON EJEMPLOS YouTube

The precedent studies on the validity of Modus ponens and Modus tollens have been carried out with most regard to a major type of conditionals in which the conditional clause is a sufficient.

Modus Tollendo Tollens i Modus Ponendo Ponens YouTube

Modus Tollens. Modus Tollens (Latin for "mode that denies" abbreviated as MT) is another form of valid inference. As in the case of MP, an instance of MT inferences involves two premises. One is again a conditional statement If A then B, while the other, unlike MP, is the negation of the consequent, i.e. a statement of the form not B.

SOLUTION Regla modus ponendo ponens y tolendo tollens Studypool

Modus Tollens. Photo by frank mckenna on Unsplash. The good sibling of modus ponens is modus tollens. Its logic looks like this: 1) If P, then Q. 2) Not Q. 3) Therefore, not P.

LÓGICA SIMBÓLICA (REGLAS DE INFERENCIA PONENDO PONENS, DOBLE NEGACIÓN Y TOLLENDO TOLLENS

In propositional logic, modus ponens (/ ˈ m oʊ d ə s ˈ p oʊ n ɛ n z /; MP), also known as modus ponendo ponens (from Latin 'method of putting by placing'), implication elimination, or affirming the antecedent, is a deductive argument form and rule of inference. It can be summarized as "P implies Q. P is true.Therefore, Q must also be true." Modus ponens is a mixed hypothetical syllogism.

PPT Predicate Logic PowerPoint Presentation, free download ID4158207

Modus tollens is a valid form of deductive argument also known as denying the consequent. Used in formal logic, modus tollens is a type of hypothetical syllogism that involves an if-then statement followed by a negation of the "then" statement (i.e., the consequent). It is typically expressed as follows: If P, then Q. Not Q.

Un ejemplo de la regla de inferencia Modus Tollens (Orión Vargas) YouTube

Modus Ponens (MP) "Modus ponens" is the Latin term for "affirmative mode." We can also call it "affirming the antecedent" because one of its premises affirms that the antecedent of the conditional is true. It is a valid form based on the concept of sufficient condition. If p is a sufficient condition of q, and p is true, then q must.

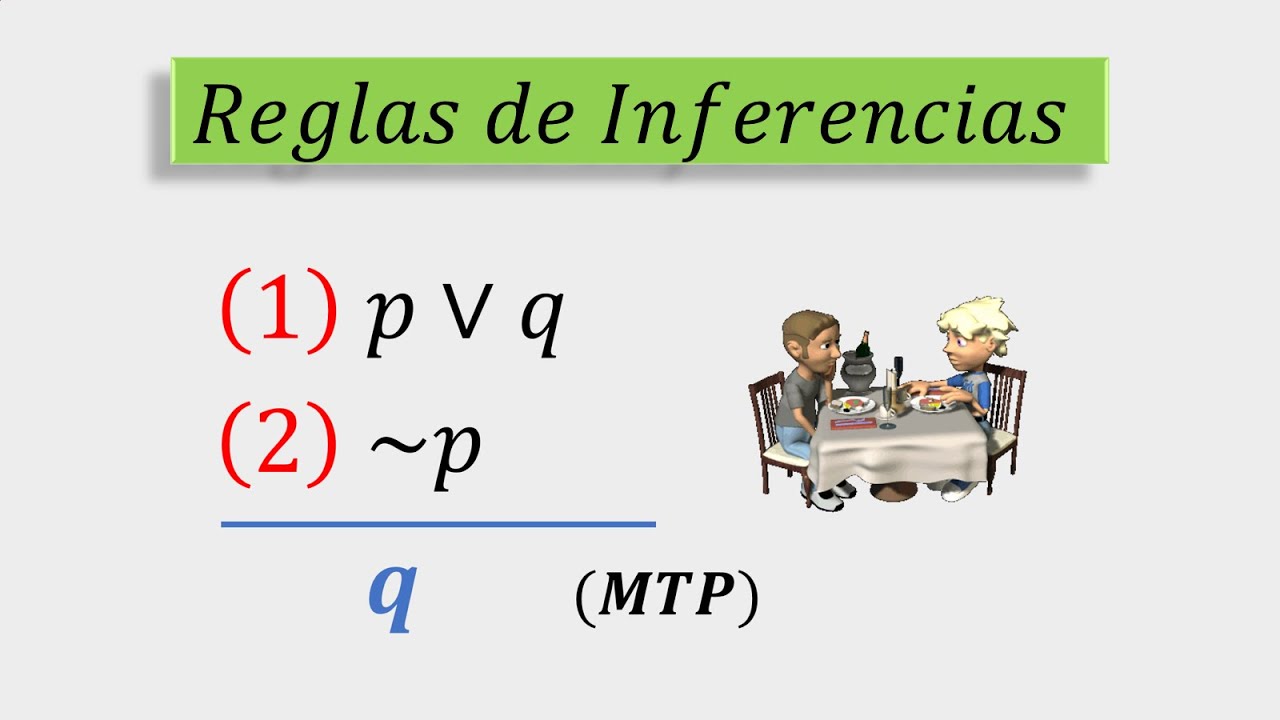
Reglas de Inferencias Silogismo disyuntivo o modus tollendo ponens YouTube

Basic Notation. In symbolic logic, modus ponens and modus tollens are two tools used to make conclusions of arguments as well as sets of arguments. We start off with an antecedent, commonly symbolized as the letter p, which is our "if" statement. Based on the antecedent, we expect a consequent from it, commonly symbolized as the letter q, which.

EL 3 N° BINARIO MODUS TOLLENDO TOLLENS

The general form of Modus Ponens is this: "If X then Y. X is true. Therefore, Y is true." Modus Tollens is a little more tricky.. (Modus Ponens), MT (Modus Tollens), DA (Denying the Antecedent) or AC (Affirming the Consequent). Don't worry about soundness this time, just focus on the form of the argument to see if it is valid or not..

The rule of Modus Tollens YouTube

Modus ponens and modus tollens are also known as syllogisms. A syllogism is an argument form wherein a deduction follows from two premises. There are two other common syllogisms, hypothetical syllogism and disjunctive syllogism. Hypothetical syllogism basically asserts a transitivity property for implications.

Modus Tollens Aturan dan Tabel Kebenarannya

The phrase "one person's modus ponens is another's modus tollens" is a popular philosophical motto that reminds us that a chain of logical reasoning works in both directions: if the truth of some premises entail the truth of a conclusion, then the falsity of the conclusion entails the falsity of at least one of the premises.. Here are some early appearances: