Transformaciones lineales IV. Imagen y nucleo de una transformacion. Profesor Yee YouTube

NÚCLEO imagen RANGO y nulidad de una TRANSFORMACIÓN LINEAL / aplicación lineal T(x,y,z)=(z,y

MI NUEVO LIBRO 🔥www.librodealgebra.com🔥 Todo mi contenido podes encontrarlo organizado en mi web 🔥https://www.algebraparatodos.com/cursos🔥 GUIA DE EJER.

Núcleo en transformaciones lineales

Para concluir la clase repasemos lo siguiente: hemos visto que la imagen es el conjunto de vectores (w) que pertenecen a un espacio vectorial (W), donde cada uno de ellos es igual a la transformación lineal de un vector (v) que pertenece a otro espacio vectorial (V). Asimismo, el núcleo es el conjunto de vectores de un espacio vectorial, tal.

🟣🟣🟣NÚCLEO E IMAGEN DE UNA TRANSFORMACIÓN LINEAL YouTube

Núcleo e imagen. Clasificación de las transformaciones lineales. Núcleo, imagen y teorema de las dimensiones. Núcleo de una transformación lineal. Sea \(F:V \to W\;\) una transformación lineal. Llamamos núcleo de \(F\) al conjunto de vectores del dominio cuya imagen por \(F\) es el \({0_W}\).

Ejemplo 1 Núcleo e imagen de una Transformación lineal YouTube

Teorema 5.7.1: One to One and Kernel. Dejar T ser una transformación lineal donde ker(T) está el núcleo de T. Entonces T es uno a uno si y solo si ker(T) consiste en solo el vector cero. Un resultado importante es la relación entre la dimensión del núcleo y la dimensión de la imagen de una transformación lineal.

Álgebra A (Ingeniería) U6 Bases del núcleo y de la imagen de una transformación lineal YouTube

Esta es la continuación del video de núcleo e imagen de una transformación lineal, esta vez vamos directo a resolver 3 ejercicios. El último ejercicio se res.

UNIDAD IV 3. NÚCLEO E IMAGEN DE UNA TRANSFORMACIÓN LINEAL YouTube

Definición 9.8.1: Kernel and Image. Dejar V y W ser espacios vectoriales y dejar T: V → W ser una transformación lineal. Entonces la imagen de T denotado como im(T) se define como el conjunto {T(→v): →v ∈ V} En palabras, consiste en todos los vectores en los W que iguales T(→v) para algunos →v ∈ V. El núcleo, ker(T), consiste.

Transformaciones lineales IV. Imagen y nucleo de una transformacion. Profesor Yee YouTube

Para aquellos de ustedes aficionados a la terminología elegante, estas acciones animadas pueden describirse como "transformaciones lineales del espacio unidimensional".La palabra "transformación" tiene el mismo significado que la palabra "función": algo que toma un número y devuelve otro, por ejemplo f (x) = 2 x ‍ .Sin embargo, mientras que típicamente visualizamos las funciones con.

Transformación Lineal. Imagen de una Transformación Lineal Conceptos Básicos. YouTube

5.5 Algebra de la Transformaciones lineales. Suma. Se define la suma C=A+B donde A y B son transformaciones lineales para hace la función C(x)=A(x)+B(x). Puede facilmente verificarse que es tambien yna transformacion lineal. Puede verificar que se dan dos transformaciones lineales A y B, tales que 1. A+B=B+A 2.

Núcleo e imagen de una transformación lineal YouTube

El nucleo (kernel, espacio nulo) de T se de ne como la preimagen completa del vector nulo: 3. Proposicion (el nucleo de una transformacion lineal es un subespacio vecto-rial del dominio). Sean V; W espacios vectoriales sobre un campo F y sea T 2 L(V; W ). Entonces ker(T ) es un subespacio de V . 4.

Álgebra lineal. Núcleo e Imagen de una transformación lineal. YouTube

Use the result matrix to declare the final solution to the system of equations. a = 0 a = 0. b = 0 b = 0. c = 0 c = 0. Write a solution vector by solving in terms of the free variables in each row. ⎡ ⎢⎣a b c⎤ ⎥⎦ = ⎡ ⎢⎣0 0 0⎤ ⎥⎦ [ a b c] = [ 0 0 0] Write as a solution set. ⎧.

Transformación Lineal. Núcleo de una Transformación Lineal Ejercicio. YouTube

MI NUEVO LIBRO 🔥www.librodealgebra.com🔥 Todo mi contenido podes encontrarlo organizado en mi web 🔥https://www.algebraparatodos.com/cursos🔥 GUIA DE EJER.

Núcleo e imagen de una transformación lineal

sobre un campo F y sea T entonces L (V, W). La imagen de T se define como el conjunto de todos los valores de la aplicacion T. El núcleo de una transformación lineal. Sean V, W espacios vectoriales. sobre un campo F y sea T ∈entonces L (V, W). El núcleo (kernel, espacio nulo) de T se define como la preimagen completa del vector nulo:

Cómo calcular la REPRESENTACIÓN MATRICIAL de una TRANSFORMACIÓN lineal NÚCLEO imagen Nulidad

El núcleo de una transformación lineal es un subespacio vectorial de V. Esto significa que cumple con las siguientes propiedades: 1. Contiene el vector nulo: El vector nulo siempre pertenece al núcleo, ya que T (0) = 0. 2. Cerrado bajo la suma: Si v₁ y v₂ son vectores en el núcleo de T, entonces su suma v₁ + v₂ también pertenece al.

BASE DEL NUCLEO E IMAGEN TEOREMA DE LA DIMENSION Transformaciones Lineales Ejercicio Resuelto

Nucleo e imagen de una transformaci on lineal 1. Objetivo. De nir el nucleo y la imagen de una transformaci on lineal, ver la relaci on con las propiedades inyectiva y sobrayectiva, estudiar ejemplos.

Núcleo e imagen de una transformación lineal YouTube

En este video explico lo que es el núcleo y la imagen de una transformación lineal. Una de las cosas más importantes que siempre se debe tener en cuenta es q.

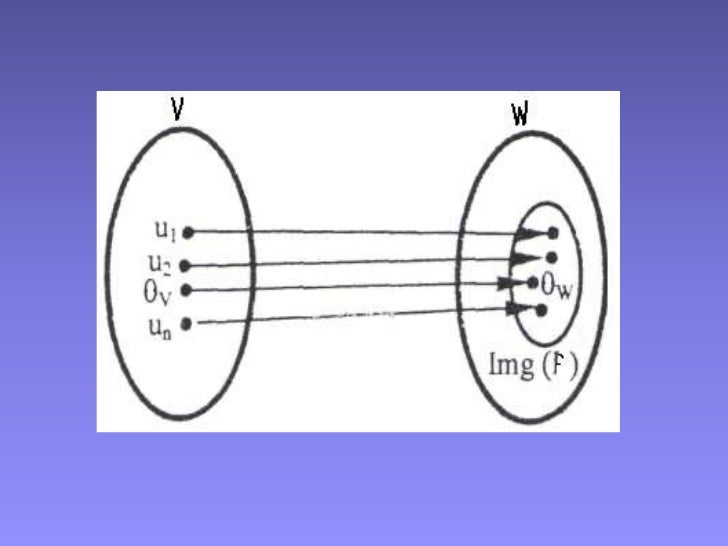
NÚCLEO E IMAGEN DE UNA TRANSFORMACIÓN LINEAL

Clase 19. Parte 1. Núcleo e imagen. 1. Núcleo e imagen. Definición: Sea T: V → W T: V → W una transformación lineal. El núcleo o kernel de T, T, denotado como núcleo(T), n ú c l e o ( T), es el conjunto de todos los vectores en V V que son mapeados por T T al 0 0 de W. W. Es decir, núcleo(T) = {v ∈ V ∣ T (v) = 0}. n ú c l e o.