3 formas de calcular el rango intercuartil wikiHow

Ahora que el entrenador Taylor tiene sus cuatro grupos, quiere encontrar el rango intercuartil para resumir mejor el desempeño de sus jugadores. Para encontrar el rango intercuartil, simplemente tome el cuartil superior y reste el cuartil inferior: 7.5 - 2.5 = 5. El rango intercuartílico para este conjunto de datos es 5.

Rango intercuartil _ AcademiaLab

El rango intercuartílico o intercuartil, a veces también abreviado como RQ o IQR, es una medida de dispersión que tiene como base las medianas del conjunto de datos. Se puede definir como la diferencia entre el tercer cuartil (Q3) y el primer cuartil (Q1). A la mitad del rango intercuartil se le conoce como desviación cuartil (DQ), y se.

¿Cómo calcular el Rango Intercuartil Datos NO Agrupados? YouTube

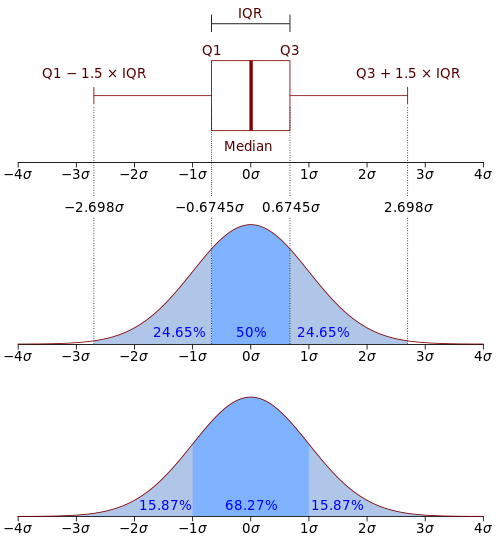
El rango intercuartil se usa a menudo para encontrar valores atípicos en los datos. Los valores atípicos aquí se definen como observaciones que caen por debajo de Q1 − 1,5 IQR o por encima de Q3 + 1,5 IQR. En un diagrama de caja, el valor más alto y más bajo que se produce dentro de este límite se indica mediante bigotes de la caja.

🔥Cómo CALCULAR el RANGO INTERCUARTIL (INTERCUARTÍLICO) en ESTADÍSTICA Rápido y FÁCIL

El rango intercuartil (IQR) es la longitud del 50% medio de ese intervalo de espacio. El rango intercuartil es el 50% medio de un conjunto de datos. Box and whiskers image by Jhguch at es.wikipedia. Si quieres saber que es el IQR en términos formales, el IQR se calcula como: La diferencia entre el tercer cuartil o superior y el primer cuartil.

3 formas de calcular el rango intercuartil wikiHow

Generalmente utilizado en el diagrama de caja que utiliza la mediana como medida central. La forma abreviada de nombrar al rango intercuartílico es RIC o RQ. El rango intercuartil utiliza la mediana como medida central. Entonces, el resultado del rango intercuartil será próximo a la mediana o segundo cuartil (Q2) si hay pocos valores extremos.

3 formas de calcular el rango intercuartil wikiHow

En las estadísticas descriptivas, el rango intercuartil (IQR) es una medida de la dispersión estadística, siendo igual a la diferencia entre el tercer y el primer cuartil.. Si el ancho establecido es mayor que el ancho de la pantalla del dispositivo, se ajustará automáticamente al 100% del ancho de la pantalla. En el modo de vista.

Medianas y rangos intercuartil de los puntajes de percepción de... Download Scientific Diagram

Resumen. En resumen, el rango intercuartílico es una medida de la dispersión y la variabilidad de un conjunto de datos que considera el rango del 50% medio de los datos y, a menudo, se denomina IQR. La fórmula IQR es. Se puede encontrar usando la mediana para dividir los datos en dos conjuntos, uno superior y otro inferior, y luego encontrar.

3 formas de calcular el rango intercuartil wikiHow

El rango intercuartil es la mitad de los datos que se encuentra entre los cuartiles superior e inferior. En otras palabras, el rango intercuartil incluye el 50% de los puntos de datos que están por encima del Q1 y por debajo del Q4. El IQR es el área roja en el gráfico de abajo, que contiene Q2 y Q3 (no etiquetados). Leer Funciones simétricas.

Calcular cuartiles y rango intercuartil en datos simples YouTube

La diferencia entre Q3 y Q1 es el rango intercuartil (IQR). Debido a que la distancia entre Q1 y Q3 incluye las dos cuartas partes medias de la distribución, los valores entre esos dos cuartiles a veces se denominan la mitad media de los datos. Cuanto más grande es el IQR, más extendido está la mitad media de los valores de los datos.

Rango intercuartílico Qué es, definición y concepto

Según la Calculadora de rango intercuartílico, el rango intercuartil (IQR) para este conjunto de datos se calcula como: Q1: 12. Q3: 26,5. IQR = Q3 - Q1 = 14.5. Esto nos dice que el 50% medio de los valores del conjunto de datos tiene un margen de 14,5 . Desviación Estándar. La desviación estándar de un conjunto de datos es una forma de.

rango intercuartil y desviación estándar YouTube

El rango intercuartílico es una medida de variabilidad adecuada cuando la medida de posición central empleada ha sido la mediana. Se define como la diferencia entre el tercer cuartil (Q 3) y el primer cuartil (Q 1 ), es decir: RQ = Q 3 - Q 1. A la mitad del rango intercuartil se le conoce como desviación cuartil (DQ), es afectada muy poco.

3 formas de calcular el rango intercuartil wikiHow

El rango intercuartílico IQR (o rango intercuartil) es una estimación estadística de la dispersión de una distribución de datos.Consiste en la diferencia entre el tercer y el primer cuartil.Mediante esta medida se eliminan los valores extremadamente alejados. El rango intercuartílico es altamente recomendable cuando la medida de tendencia central utilizada es la mediana (ya que este.

3 formas de calcular el rango intercuartil wikiHow

El siguiente video cuenta con la explicación de:- Definición del Rango (o Amplitud) y del Rango Intercuartil.- Cálculo del Rango y del Rango Intercuartil a t.

Cómo calcular el rango intercuartil en Google Sheets en 2024 → STATOLOGOS®

El RIQ es el "rango intercuartil" de un conjunto de datos. Se utiliza en el análisis estadístico para ayudar a obtener conclusiones acerca de un conjunto de números. El RIQ a menudo se utiliza más que el rango, porque excluye la mayoría de los valores atípicos. ¡Continúa leyendo para aprender a calcular el RIQ!

Cuartiles y Rango Intercuartilico Ejemplo 2 YouTube

Comparar el rango y el rango intercuartil (RIQ) El rango y el rango intercuartil (RIQ) miden la "dispersión" de un conjunto de datos. Mirar la dispersión nos permite ver qué tanto varían los datos. El rango es una manera rápida de tener una idea de la dispersión. Lleva más tiempo encontrar el RIQ, pero a veces nos da información más.

Cómo encontrar valores atípicos utilizando el rango intercuartil en 2021 → VACANCEENEUROPE®

El rango semi-intercuartil es un medio de la diferencia entre el primer y tercer cuartiles. Es la mitad de la distancia requerida para cubrir la mitad de las cuentas. El rango semi-intercuartil es afectado muy poco por cuentas extremas. Esto lo hace una buena medida de dispersión para distribuciones sesgadas. Se obtiene evaluando .